反函数定理,反函数定理,解析函数及其反函数的奥秘
反函数定理指出,如果函数f在开集D上连续可导,且其导数f'在D上非零,则f在D上是一一对应的,并且存在反函数f⁻¹,这个反函数在f的值域上也是连续可导的,并且其导数f⁻¹'满足f⁻¹'(y) = 1 / f'(x),其中x是f⁻¹(y)对应的原函数值,该定理为求解反函数及其性质提供了理论基础。
大家好,今天我想和大家聊聊数学中的一个重要概念——反函数定理,其实这个定理在高中数学就已经接触过了,但是当时感觉挺抽象的,现在回想起来,这个定理还挺有趣的,反函数定理就是告诉我们,如果一个函数是单调的,那么它就一定存在一个反函数,听起来很简单,但是它的应用范围却非常广泛,比如在经济学、物理学等领域都有很重要的应用。
我就从几个来地讲解一下反函数定理。
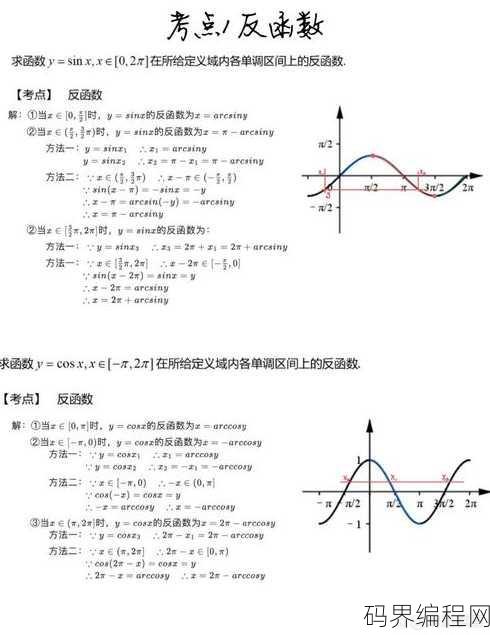
一:什么是反函数定理?
- 定义:反函数定理是指,如果一个函数( f(x) )在某个区间内是单调的,那么它就一定存在一个反函数( f^{-1}(x) ),且这个反函数也是单调的。
- 条件:单调性是反函数定理存在的前提条件,单调性可以分为单调递增和单调递减两种情况。
- 应用:在数学分析、微分方程、数值计算等领域,反函数定理都有着广泛的应用。
二:反函数定理的证明
- 假设:假设函数( f(x) )在区间( I )内是单调递增的。
- 定义反函数:对于任意( y \in f(I) ),定义反函数( f^{-1}(y) )为满足( f(f^{-1}(y)) = y )的( x )值。
- 证明过程:
- 单调性:假设( x_1, x_2 \in I ),且( x_1 < x_2 ),由于( f(x) )是单调递增的, f(x_1) < f(x_2) )。
- 反函数的存在性:对于任意( y \in f(I) ),由于( f(x) )是单调递增的, f^{-1}(y) )唯一。
- 反函数的单调性:假设( y_1, y_2 \in f(I) ),且( y_1 < y_2 ),由于( f(x) )是单调递增的, f^{-1}(y_1) < f^{-1}(y_2) )。
三:反函数定理的应用
- 数值计算:在数值计算中,反函数定理可以用来求解方程( f(x) = y )的近似解。
- 优化问题:在优化问题中,反函数定理可以用来求解最优解。
- 物理学:在物理学中,反函数定理可以用来求解某些物理量的变化率。
四:反函数定理的推广
- 多元函数:对于多元函数,反函数定理可以推广为反函数定理的推广形式。
- 多变量函数:在多变量函数中,反函数定理可以用来求解函数的极值问题。
- 非线性方程组:在非线性方程组中,反函数定理可以用来求解方程组的解。
五:反函数定理的局限性
- 不满足单调性:如果一个函数不是单调的,那么它就不一定存在反函数。
- 定义域和值域:反函数的存在性还需要考虑函数的定义域和值域。
- 应用场景:反函数定理在某些特定场景下可能不适用。
反函数定理是一个非常重要的数学概念,它不仅可以帮助我们解决一些实际问题,还可以拓宽我们的数学视野,希望这篇文章能够让大家对反函数定理有一个更深入的了解。
其他相关扩展阅读资料参考文献:
定义与核心思想
- 反函数定理是数学分析中研究函数可逆性的重要工具,其核心在于通过原函数的性质判断其反函数是否存在,并推导反函数的导数表达式。
- 定理的核心思想是:若函数在某点处可微且导数不为零,则其在该点附近存在反函数,且反函数的导数可通过原函数的导数计算。
- 这一定理将函数的局部可逆性与导数的非零性直接关联,为后续的微分学应用提供了理论基础。
存在性条件的数学解析
- 可微性是反函数定理的前提条件,函数必须在定义域内某点的邻域内可微,才能保证其局部行为足够“平滑”。
- 导数非零是关键判据:若原函数在某点的导数为零,则函数在该点可能无法保持单射性,从而导致反函数不存在,函数 $ f(x) = x^3 $ 在 $ x = 0 $ 处导数为零,但其反函数仍存在,说明该条件需结合其他因素分析。
- 局部可逆性要求函数在某点的邻域内是单射的,即满足严格单调性。$ f(x) = e^x $ 在整个实数域上严格单调递增,因此其反函数 $ \ln x $ 全局存在;而 $ f(x) = x^3 $ 在 $ x = 0 $ 附近虽导数为零,但因严格单调性仍局部可逆。
几何意义与直观理解
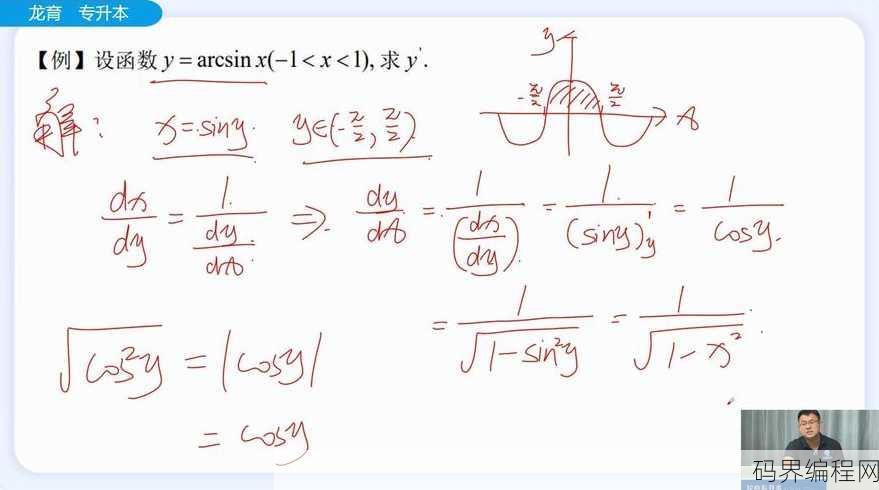
- 图像对称性:反函数的图像与原函数的图像关于直线 $ y = x $ 对称,这一特性在几何上直观体现了函数与反函数的互逆关系。
- 切线斜率的倒数关系:若原函数在某点的切线斜率为 $ f'(a) $,则反函数在对应点的切线斜率为 $ \frac{1}{f'(a)} $,函数 $ f(x) = 2x + 3 $ 在 $ x = 1 $ 处的导数为2,其反函数 $ f^{-1}(x) = \frac{x - 3}{2} $ 在 $ y = 5 $ 处的导数为 $ \frac{1}{2} $。
- 单调性与可逆性:严格单调函数的图像不会出现“回折”,因此必然存在反函数,正弦函数在区间 $ (-\frac{\pi}{2}, \frac{\pi}{2}) $ 上严格单调递增,其反函数 $ \arcsin x $ 在该区间内存在。
应用领域的实际案例
- 微积分中的变量替换:在积分计算中,反函数定理常用于变量替换法,例如求解 $ \int \frac{1}{\sqrt{1 - x^2}} dx $ 时,通过反函数 $ \arcsin x $ 的导数公式简化过程。
- 物理中的运动学分析:当研究物体运动时,若已知位移与时间的函数关系,可通过反函数定理求得时间与位移的反函数,从而分析速度或加速度的反向关系,自由落体运动的位移函数 $ s(t) = \frac{1}{2}gt^2 $ 的反函数 $ t(s) = \sqrt{\frac{2s}{g}} $ 可用于计算特定位移对应的时间。
- 经济学中的供需模型:在需求函数 $ Q = D(P) $ 中,若价格 $ P $ 与数量 $ Q $ 的关系满足反函数定理的条件,可通过反函数求得价格与数量的反向关系,便于分析市场均衡点,需求函数 $ Q = 100 - 2P $ 的反函数 $ P = 50 - \frac{Q}{2} $ 直接反映了价格对数量的依赖性。
反函数定理的证明与延伸
- 证明的关键步骤:定理证明通常基于隐函数定理,通过构造辅助函数并利用微分的线性近似,证明反函数在邻域内存在且可导。
- 逆函数导数公式的推导:设 $ y = f(x) $,则 $ x = f^{-1}(y) $,对两边关于 $ x $ 求导,利用链式法则可得 $ \frac{dx}{dy} = \frac{1}{f'(x)} $,即 $ \frac{d}{dy}f^{-1}(y) = \frac{1}{f'(f^{-1}(y))} $,这一公式在计算反函数导数时至关重要。
- 高阶导数的计算:反函数定理不仅适用于一阶导数,还可推广至高阶导数,若 $ f(x) $ 的二阶导数存在且非零,反函数 $ f^{-1}(y) $ 的二阶导数可通过递推公式计算,这在优化问题中具有重要价值。
- 多变量函数的推广:在多元微积分中,反函数定理被扩展为隐函数定理,要求雅可比矩阵的行列式非零,以确保函数在局部可逆,函数 $ F(x, y) = 0 $ 在满足 $ \frac{\partial F}{\partial y} \neq 0 $ 时,可解出 $ y $ $ x $ 的反函数。
- 实际应用中的注意事项:在应用反函数定理时需注意定义域的限制,函数 $ f(x) = x^3 $ 的反函数在全局存在,但在 $ x = 0 $ 处导数为零,需通过分段讨论或调整定义域来满足定理条件。
反函数定理的局限性与突破
- 非光滑函数的例外:若函数在某点不可微(如分段函数的拐点),反函数定理无法直接应用,需通过其他方法分析可逆性。
- 导数为零的特殊处理:当原函数在某点导数为零时,反函数可能存在但需额外验证。$ f(x) = x^3 $ 在 $ x = 0 $ 处导数为零,但其反函数仍存在,说明定理的条件并非绝对必要。
- 非局部可逆性:即使导数非零,若函数整体不满足单射性(如 $ f(x) = x^3 - 3x $),反函数也不存在,需通过单调性分析或图像观察确定局部可逆区间。
- 多变量函数的复杂性:在多元情况下,反函数定理要求雅可比矩阵的行列式非零,但实际应用中需进一步验证函数的可逆性,例如通过泰勒展开或数值计算。
- 现代数学的拓展:反函数定理在微分几何和泛函分析中被进一步推广,用于研究流形映射、Banach空间中的可逆算子等,体现了其理论深度与应用广度。
反函数定理的教育意义
- 培养数学思维:反函数定理要求学生理解函数的局部性质与整体行为的关系,有助于培养严谨的数学逻辑。
- 连接理论与实践:通过实际案例(如物理、经济模型),学生能直观感受定理的实际价值,避免抽象概念的孤立学习。
- 强化导数应用:定理将导数与函数的可逆性直接关联,使学生掌握导数在分析函数性质中的关键作用。
- 激发问题解决能力:在应用过程中,学生需结合定理条件判断反函数是否存在,锻炼了分析问题和解决问题的能力。
- 为后续学习奠基:反函数定理是学习隐函数定理、参数方程求导等高级内容的基础,为深入理解微积分提供了理论支撑。
反函数定理不仅是数学分析的基石,更是连接理论与实践的桥梁,其核心在于通过导数的非零性判断函数的可逆性,并为反函数的导数提供计算方法,无论是单变量还是多变量函数,这一定理都展现了数学的简洁性与深刻性,在实际应用中,反函数定理帮助我们解决变量替换、模型分析等复杂问题,同时其证明过程也体现了数学推导的严谨性,理解反函数定理,不仅能提升数学素养,更能为科学与工程领域的深入研究打开大门。
“反函数定理,反函数定理,解析函数及其反函数的奥秘” 的相关文章
源程序清单是什么意思,源程序清单解析,理解源代码的蓝本
源程序清单,指的是一个程序或软件的原始代码的详细列表,它包含了构成该程序的所有指令和代码片段,通常用于开发者查看、修改或理解程序的工作原理,源程序清单是软件开发的基石,对于软件的维护、升级和功能扩展至关重要,在编程领域,源程序清单以文本文件形式存在,通常以特定的编程语言编写,如C、Java、Pyth...
sumif怎么用3个条件,Sumif函数应用技巧,同时满足三个条件的使用方法
SUMIF函数在Excel中用于根据多个条件筛选数据,要使用SUMIF函数满足三个条件,可以将这三个条件分别作为参数输入,如果要在A列、B列和C列分别检查条件1、条件2和条件3,可以使用以下公式:,``excel,=SUMIF(A:A, 条件1, B:B) + SUMIF(A:A, 条件2, B:B...
php中文网17期,PHP中文网第17期,深入探索PHP世界
《php中文网17期》内容摘要:,本期《php中文网》聚焦PHP技术领域的最新动态,深入探讨了PHP7.4的新特性,分享了优化PHP性能的实用技巧,还介绍了如何使用PHP进行微服务架构设计,以及如何利用容器化技术提升PHP应用的部署效率,栏目还涉及了安全编程的最佳实践和数据库优化的策略,本期内容旨在...
计算机编程语言有哪几种类型,计算机编程语言类型概览
计算机编程语言主要分为以下几类:1. 机器语言:直接由计算机硬件执行,是最基础的编程语言,2. 汇编语言:以助记符形式表示机器语言,易于理解,3. 高级语言:如C、C++、Java、Python等,更接近人类语言,易于编写和维护,4. 面向对象语言:如Java、C++、C#等,强调对象和类的概念,5...
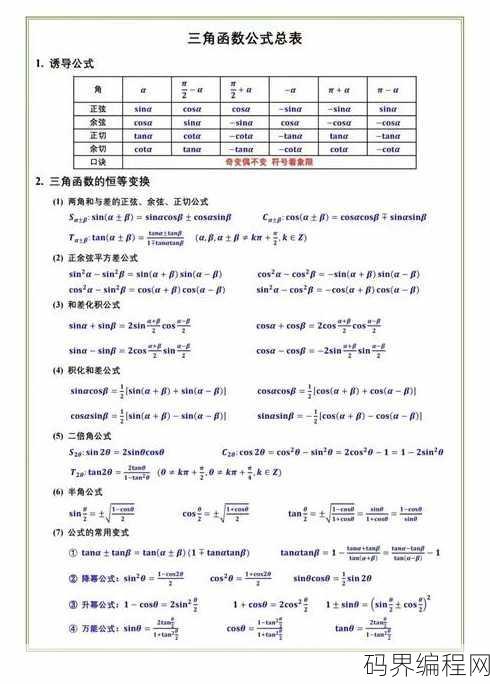
三角形的函数公式大全,三角形函数公式全面解析
《三角形的函数公式大全》是一本综合性的数学参考书籍,收录了三角形中常见的各种函数公式,书中涵盖了正弦、余弦、正切、余切、正割、余割等基本三角函数,以及它们的倒数和反函数,还包括了三角恒等式、和差公式、倍角公式、半角公式等高级公式,本书旨在为读者提供全面、便捷的三角函数公式查询工具,适用于学习、教学和...
deletefile 错误码5,解决deletefile错误码5,常见原因及修复方法
"错误码5在deletefile操作中通常表示文件删除失败,这可能由于文件正在使用中、权限不足、文件路径错误或文件系统错误等原因导致,解决此问题需要检查文件状态、权限设置,确保文件未被其他程序占用,并确认文件路径正确无误。"深入解析“deletefile 错误码5”:常见问题及解决方案 用户解答...